Introduction to Trigonometry Class 10 MCQ is one of the best strategies to prepare for the CBSE Class 10 Board exam. If you want to complete a grasp concept or work on one’s score, there is no method except constant practice. Students can improve their speed and accuracy by doing more MCQ on Introduction to Trigonometry class 10, which will help them all through their board test.
Introduction to Trigonometry Class 10 MCQ Question with Answers
Class 10 Math MCQ with answers are given here to chapter 8 Introduction to Trigonometry . These MCQs are based on the latest CBSE board syllabus and relate to the latest Class 10 Mathematics syllabus. By Solving these Class 10 MCQs, you will be able to analyze all of the concepts quickly in the chapter and get ready for the Class 10 Annual exam.
Learn Introduction to Trigonometry Class 10 MCQ with answers pdf free download according to the latest CBSE and NCERT syllabus. Students should prepare for the examination by solving CBSE Class 10 Mathematics Quadratic Equation MCQ with answers given below.
Question 1. If 4tanΘ = 1, find the value of 4sinΘ – 2cosΘ / 4sinΘ + 3cosΘ
(a) 1/2
(b) 1/6
(c) 2/3
(d) 1/3
Answer
B
Question 2. Find the value of 5cos α – 4 / 3 + 5sin α / 3 – 5sin α / 4 + 5cos α
(a) – 1
(b) 5
(c) 1
(d) 0
Answer
D
Question 3. What is the value of sin2 5o + sin2 10o + sin2 80o + sin2 85o ?
(a) 0
(b) 1
(c) 2
(d) 3
Answer
C
Question 4. If tan 26o tan19o/ x(1 tan 26o tan19o ) = cos60o, what is the value of x ?
(a) 1
(b) 2
(c) 2
(d) 3
Answer
C
Question 5. Find the value sin2 30o cos2 45o + 4tan2 30o + 1/2 sin2 90o 2cos2 90o + 1/24
(a) 1
(b) 2
(c) √2
(d) √3
Answer
B
Question 6. An electric pole is 10√3 m high and its shadow is 10 m in length, then the angle of elevation of the sun is
(a) 45°
(b) 15°
(c) 30°
(d) 60°
Answer
D
Question 7. If sin A + sin2 A = 1 , find the value of the expression (cos2 A + cos4 A) .
(a) 1
(b) 1/2
(c) 2
(d) 3
Answer
A
Question 8. Find the value of sin 15o .
(a) √3+1/√2
(b) √3 -1/√2
(c) √3+1/2√2
(d) √3 -1/2√2
Answer
D
Question 9. A kite is flying at a height of 200 m above the groun(d) The string attached to the kite is temporarily tied to a point on the groun(d) The inclination of the string with the ground is 45°. The length of the string, assuming that there is no slack in the string is
(a) 100 m
(b) 200 m
(c) 200√2 m
(d) 100√2 m
Answer
C
Question 10. The _____________ is the line drawn from the eye of an observer to the point in the object viewed by the observer.
(a) Horizontal line
(b) line of sight
(c) None of these
(d) Vertical line
Answer
B
Question 11. A kite is flying at a height of 90 m above the groun(d) The string attached to the kite is temporarily tied to a point on the groun(d) The inclination of the string with the ground is 60° . The length of the string, assuming that there is no slack in the string is
(a) 90√3 m
(b) 60√3 m
(c) 90 m
(d) 45 m
Answer
B
Question 12. If the angle of depression of a car from a 100 m high tower is 45°, then the distance of the car from the tower is
(a) 100 m
(b) 200 m
(c) 100√3m
(d) 100√2m
Answer
A
Question 13. The ___________ is the angle between the horizontal and the line of sight to an object when the object is below the horizontal level.
(a) angle of projection
(b) angle of elevation
(c) None of these
(d) angle of depression
Answer
D
Question 14. The ratio between the height and the length of the shadow of a pole is √3: 1, then the sun’s altitude is
(a) 45°
(b) 30°
(c) 75°
(d) 60°
Answer
D
Question 15. A pole 10 m high cast a shadow 10 m long on the ground, then the sun’s elevation is
(a) 60°
(b) 15°
(c) 45°
(d) 30°
Answer
C
Question 16. Two men are on opposite sides of a tower. They observe the angles of elevation of the top of the tower as 30° and 45° respectively. If the height of the tower is 100m, then the distance between them is
(a) 100(√3−1) m
(b) 100(√3+1) m
(c) 100(1−√3) m
(d) none of these
Answer
B
Question 17. From a point on the ground which is 15m away from the foot of a tower, the angle of elevation is found to be 60° . The height of the tower is
(a) 15√3 m
(b) 20√m
(c) 10√m
(d) 10 m
Answer
A
Question 18. From a point P on the level ground, the angle of elevation of the top of a tower is . If the tower is 100m high, the distance between P and the foot of the tower is
(a) 300√3 m
(b) 150√3 m
(c) 200√3 m
(d) 100√3 m
Answer
D
Question 19. The angle of elevation of the top of a tower from a point on the ground and at a distance of 30°m from its foot is . The height of the tower is
(a) 30√3m
(b) 10 m
(c) 10√3m
(d) 30 m
Answer
C
Question 20. The ___________ of an object is the angle formed by the line of sight with the horizontal when the object is above the horizontal level.
(a) angle of projection
(b) angle of depression
(c) angle of elevation
(d) none of these
Answer
A
Question 21. If the shadow of a boy ‘x’ metres high is 1.6m and the angle of elevation of the sun is then the value of ‘x’ is 45°
(a) 0.8 m
(b) 1.6 m
(c) 3.2 m
(d) 2 m
Answer
B
Question 22. If the angle of depression of an object from a 75m high tower is 30° , then the distance of the object from the tower is
(a) 25√3 m
(b) 50√3 m
(c) 100√3 m
(d) 75√3 m
Answer
D
Question 23. If the height of the tower is √3 times of the length of its shadow, then the angle of elevation of the sun is
(a) 15°
(b) 30°
(c) 50°
(d) 45°
Answer
C
Question 24. A ramp for disabled people in a hospital must slope at not more than 30°. If the height of the ramp has to be 1 m, then the length of the ramp be
(a) 3 m
(b) 1 m
(c) 2 m
(d) √3 m
Answer
C
Question 25. The angles of elevation of the top of a tower from two points on the ground at distances 8 m and 18 m from the base of the tower and in the same straight line with it are complementary. The height of the tower is
(a) 12 m
(b) 18 m
(c) 8 m
(d) 16 m
Answer
A
Question 26. In a right triangle ABC, If AC = BC and then find its value
(a) 50√3
(b) 150 m
(c) None of these
(d) 100√3 m
Answer
D
Question 27. The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If the tower is 50m high, then the height of the hill is
(a) 50√3 m
(b) 150m
(c) 150√3 m
(d) 100√3 m
Answer
B
Whoever needs to take the CBSE Class 10 Board Exam should look at this MCQ. To the Students who will show up in CBSE Class 10 Mathematics Board Exams, It is suggested to practice more and more questions. Aside from the sample paper you more likely had solved. These Introduction to Trigonometry class 10 MCQ are ready by the subject specialists themselves.
Question 28. Find the value of cos1o cos2o cos3o …..cos89o cos90o
(a) 1
(b) 1/2
(c) 1/√2
(d) 0
Answer
D
Question 29. Find the value of 2/3 (cos4 30o – sin4 45o ) – 3 (sin2 60o – sec2 45o ) + 1/4 cot2 30o
(a) 15/4
(b) 3/4
(c) 2(65/4)
(d) 4(17/24)
Answer
D
Question 30. If cos9α = sinα a and 9α < 90o, what is the value of tan 5 a?
(a) 1/√3
(b) √3
(c) 1
(d) 1/2
Answer
C
Question 31. ABCD is a trapezium in which AB = 8 cm, AD = 4 cm and CD = 3 cm.
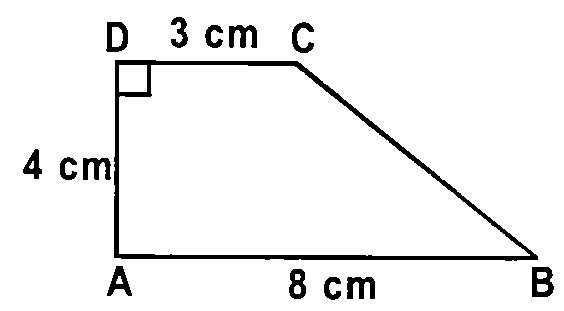
What is the length of BC to the nearest whole number?
(a) 5 cm
(b) √41cm
(c) 8 cm
(d) 7 cm
Answer
B
Question 32. If ΔABC is right angled at C, find the value of cos(A + B) .
(a) 0
(b) 1
(c) 1/2
(d) √3/2
Answer
A
Question 33. What is the value of sin2 5o + sin2 10o + sin2 80o + sin2 85o ?
(a) 0
(b) 1
(c) 2
(d) 3
Answer
C
Question 34. If 8 tan A =15, find the value of sinA – cosA / sinA + cosA
(a) 7/23
(b) 11/23
(c) 13/23
(d) 17/23
Answer
A
Question 35. If 4sinΘ = 3cosΘ ,find sec2Θ / 4(1 – tan2Θ)
(a) 25/16
(b) 25/28
(c) 1/4
(d) 5/6
Answer
B
Question 36. If the shadow of a tower is 30 m long when the sun’s elevation is . The length of the shadow, when the sun’s elevation is
(a) 10 m
(b) 30 m
(c) 10√3 m
(d) 20 m
Answer
A
Question 37. Two men are on opposite sides of a tower. They observe the angles of elevation of the top of the tower as 60° and 45° respectively. If the height of the tower is 60m, then the distance between them is
(a) 20(√3−√3)m
(b) 20(√3−√3)m
(c) None of these
(d) 20(√3+√3)m
Answer
D
Question 38. If tan 26o tan19o/ x(1 tan 26o tan19o ) = cos60o, what is the value of x ?
(a) 1
(b) 2
(c) 2
(d) 3
Answer
C
Question 39. If 4tanΘ = 1, find the value of 4sinΘ – 2cosΘ / 4sinΘ + 3cosΘ
(a) 1/2
(b) 1/6
(c) 2/3
(d) 1/3
Answer
B
Question 40. If the altitude of the sun is 60° , the height of a tower which casts a shadow of length 90 m is
(a) 60 m
(b) 90√3 m
(c) 90 m
(d) 60√3 m
Answer
B
Question 41. Find the value of 5cos α – 4 / 3 + 5sin α / 3 – 5sin α / 4 + 5cos α
(a) – 1
(b) 5
(c) 1
(d) 0
Answer
D
Question 42. A river is 60 m wide. A tree of unknown height is on one bank. The angle of elevation of the top of the tree from the point exactly opposite to the foot of the tree, on the other bank, is 30°. The height of the tree is
(a) 30√3 m
(b) 10√3 m
(c) 20√3 m
(d) 60√3 m
Answer
C
Question 43. A plane is observed to be approaching the airport. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 30° there at. Its height above the ground is
(a) 10 km
(b) 12 km
(c) 6 km
(d) none of these
Answer
C
Question 44. Find the value sin2 30o cos2 45o + 4tan2 30o + 1/2 sin2 90o 2cos2 90o + 1/24
(a) 1
(b) 2
(c) √2
(d) √3
Answer
B
Question 45. If cos9α = sinα a and 9α < 90o, what is the value of tan 5 a?
(a) 1/√3
(b) √3
(c) 1
(d) 1/2
Answer
C
Question 46. If sin A + sin2 A = 1 , find the value of the expression (cos2 A + cos4 A) .
(a) 1
(b) 1/2
(c) 2
(d) 3
Answer
A
Question 47. Find the value of sin 15o .
(a) √3+1/√2
(b) √3 -1/√2
(c) √3+1/2√2
(d) √3 -1/2√2
Answer
D
Question 48. Find the value of 2/3 (cos4 30o – sin4 45o ) – 3 (sin2 60o – sec2 45o ) + 1/4 cot2 30o
(a) 15/4
(b) 3/4
(c) 2(65/4)
(d) 4(17/24)
Answer
D
Question 49. If 8 tan A =15, find the value of sinA – cosA / sinA + cosA
(a) 7/23
(b) 11/23
(c) 13/23
(d) 17/23
Answer
A
Question 50. ABCD is a trapezium in which AB = 8 cm, AD = 4 cm and CD = 3 cm.
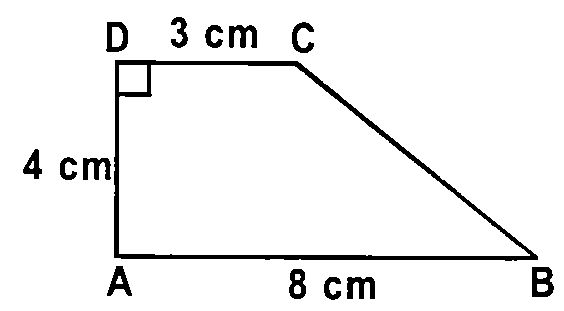
What is the length of BC to the nearest whole number?
(a) 5 cm
(b) √41cm
(c) 8 cm
(d) 7 cm
Answer
B
Question 51. Find the value of cos1o cos2o cos3o …..cos89o cos90o
(a) 1
(b) 1/2
(c) 1/√2
(d) 0
Answer
D
Question 52. What is the angle between the hour and minute hands of a clock at 02 :15 hours?
(a) 15o
(b) 7 (1o/2)
(c) 22(1o/2)
(d) 30o
Answer
C
Question 53. If 4sinΘ = 3cosΘ ,find sec2Θ / 4(1 – tan2Θ)
(a) 25/16
(b) 25/28
(c) 1/4
(d) 5/6
Answer
B
Question 54. If ΔABC is right angled at C, find the value of cos(A + B) .
(a) 0
(b) 1
(c) 1/2
(d) √3/2
Answer
A
You can easily get good marks If you study with the help of Class 10 Introduction to Trigonometry MCQ. We trust that information provided is useful for you. NCERT MCQ Questions for Class 10 Introduction to Trigonometry PDF Free Download would without a doubt create positive results.
We hope the information shared above in regards to MCQ on Introduction to Trigonometry Class 10 with Answers has been helpful to you. if you have any questions regarding CBSE Class 10 Mathematics Solutions MCQs Pdf, write a comment below and we will get back to you as soon as possible.
Frequently Asked Question (FAQs)
How many MCQ questions are there in Class 10 Chapter 8 Mathematics?
In Class 10 chapter 8 Mathematics, we have provided 54 Important MCQ Questions, But in the future, we will add more MCQs so that you can get good marks in the Class 10 exam.
Can we score good marks in Class 10 Mathematics with the help of Introduction to Trigonometry MCQ Questions?
Yes, MCQ Question is one of the best strategies to make your preparation better for the CBSE Board Exam. It also helps to know the student’s basic understanding of each chapter. So, You can score good marks in the Class 12 Mathematics exam.