Class 11 Mathematics Chapter 11 Conic Sections MCQ Questions with Answer

Conic Sections Class 11 MCQ is one of the best strategies to prepare for the CBSE Class 11 Board exam. If you want to complete a grasp concept or work on one’s score, there is no method except constant practice. Students can improve their speed and accuracy by doing more Conic Sections class 11 MCQ which will help them all through their board test.

Conic Sections Class 11 MCQ Questions with Answer

Class 11 Math MCQ with answers are given here to Chapter 11 Conic Sections. These MCQs are based on the latest CBSE board syllabus and relate to the latest Class 11 Mathematics syllabus. By Solving these Class 11 MCQs, you will be able to analyze all of the concepts quickly in the Chapter and get ready for the Class 11 Annual exam.

Learn Conic Sections Class 11 MCQ with answers pdf free download according to the latest CBSE and NCERT syllabus. Students should prepare for the examination by solving CBSE Class 11 Conic Sections MCQ with answers given below.

Question 1: The latusrectum of the parabola y²=5x+4y+1 is
(a) 5/4
(b) 10
(c) 5
(d) 5/2Answer

A

Question 2: The equation of parabola having vertex ( , )0 0 , passing through (5 , 2) and symmetric with respect to y-axis is
(a) 3x²=25y
(b) 2x²=25y 
(c) 2y²=25x
(d) None of theseAnswer

B

Question 3: x -2=t²,y=2t are the parametric equations of the parabola
(a) y²=4x
(b) y²==-4x
(c) x²=-4y
(d) y²==4(x-2)Answer

D

Question 4: If the point P(4,2)  is one end of the focal chord PQ of the parabola y²=x,  then the slope of the tangent at Q is
(a) -1/4
(b) 1/4
(c) 4
(d) -4Answer

C

Question 5: The equation of the parabola having vertex at the origin axis on the y-axis and passing through the point(6 ,3)  is
(a) y²=12x+6 
(b) x²=12y y 2
(c) x²=-12y 
(d) y²=-12x+6

Question 6. If one end of a diameter of the circle x² + y² – 4x – 6y + 11 = 0 is (3, 4), then find the coordinate of the other end of the diameter.
(a) (2, 1)
(b) (1, 2)
(c) (1, 1)
(d) None of theseAnswer

B

Question 7. The centre of a circle is (2, – 3) and the circumference is 10p. Then, the equation of the circle is
(a) x² + y² + 4x + 6y +12 = 0
(b) x² + y² – 4x + 6y +12 = 0
(c) x² + y² – 4x + 6y -12 = 0
(d) x² + y² – 4x – 6y -12 = 0Answer

C

Question 8: If the vertex of a parabola is the point(-3,0 ) and the directrix is the line x +5= 0, then equation of parabola is
(a) y²=8(x+3) x 2
(b) x²=8(y+3)
(c) y²=-8(x+3 x 2
(d) y²=8(x+5) x 2 Answer

A

Question 9: The focus of the parabola y²=4y-4x  is
(a) (0, 2)
(b) (1, 2)
(c) (2, 0)
(d) (2, 1)Answer

A

Question 10: The equation λx²+4xy+y²+ λx+3y+2=0 parabola, if λ is
(a) -4
(b) 4
(c) 0
(d) None of these Answer

B

Question 11: The length of latusrectum of the parabola 169 {(x-1)²+(y-3)²}=(5x-12y+17)²  is
(a) 14/13
(b) 28/13
(c) 12/13
(d) None of these

Question 12: The equation of tangent to the parabola y²=9x x 2  which goes throughthe point (4, 10), is
(a) x+4y+1=0 
(b) 9x+4y+4=0 
(c) x-4y+36=0 
(d) 9x+4y+9=0 Answer

C

Question 13: The tangent to the parabola y²=4ax at the point( a,2a) makes with x-axis an angle equal to
(a) π/3
(b) π/4
(c) π/2
(d)π/6Answer

B

Question 14: If the tangent at the point P(2,) 4 to the parabola y²=8x meets the parabola y²=8x+5ay Q and R, then the mid-point of the QR is
(a) (2, 4)
(b) (4,2)
(c) (7, 9)
(d) None of theseAnswer

B

Question 15: At what point on the parabola y²=4x,the normal makes equal angles with the coordinate axes?
(a) (4, 4)
(b) (9, 6)
(c) (4,-4)
(d) (1,-2) Answer

D

Question 16: The circle x²+y²=5 meets the parabola y²=4x at P and Q . Then, the length PQ is equal to
(a) 2
(b) 2√2
(c) 4
(d) None of these Answer

C

Question 17: The normal at three points P, Q, R of the parabola y²=4ax  meet in (h k). The centroid of Δ PQR lies on
(a) x = 0
(b) y = 0
(c) x=-a
(d) y=a 

Question 18: The tangents and normal at the ends of the latusrectum of a parabola form a
(a) cyclic quadrilateral
(b) rectangle
(c) square
(d) None of theseAnswer

C

Question 19: The locus of the middle points of the focal chords of parabola
y2=4ax  is
(a) y²=a(x-a) 
(b) y²=2a(x-a)
(c) y² =4a(x-a)
(d) None of these Answer

B

Question 20: If the normal to the parabola y²=4ax at the point P(at², 2at) cuts the parabola again at Q(aT²,2aT aT), then
(a) – 2≤ T ≤2
(b) T∈(-∞,-8) ∪ (8,∞)
(c) T² < 8
(d) T² ≤ 8 Answer

D

Question 21: A tangent to a parabola y2=4 ax  is inclined at π/3 with the axis of the parabola. The point of contact is

Answer

A

Question 22: If tangents at A and B on the parabola y²=4ax intersect at point C,then ordinates of A C, and B are
(a) always in AP
(b) always in GP
(c) always in HP
(d) None of these

Question 23. The range of a, for which the point (a, a) lies inside the region bounded by the curves y = √1 – x² and x + y = 1 is
(a) 1/2 < α < 1/√2
(b) 1/2 < α < 1/3
(c) 1/3 < α < 1/√3
(d) 1/4 < α < 1/2Answer

A

Question 24. A line meets the coordinate axes in A and B.A circle is circumscribed about the DOAB. The distances from the points A and Bof the side ABto the tangent at O are equal to mand n respectively. Then, the diameter of the circle is
(a) m(m + n)
(b) n(m + n)
(c) m – n
(d) None of theseAnswer

D

Question 25. Let L1 be a straight line passing through the origin and L2 be the straight line x + y = 1. If the intercepts made by the circle x² + y² – x + 3y = 0 on L₁L₂ and are equal, then L1 can be represented by
(a) x + y = 0
(b) x – y = 0
(c) 7x + y = 0
(d) x – 7y = 0Answer

B

Question 26. The set of values of c so that the equations y =|x|+ c and x² + y² – 8|x|- 9 = 0 have no solution, is
(a) (-∞, – 3) È (3, ∞)
(b) (-3, 3)
(c) (-∞, 5 2) È (5 2, ∞)
(d) (5 2 – 4, ∞)Answer

D

Question 27. The range of values of a such that the angle q between the pair of tangents drawn from(a, 0) to the circle x² + y² = 1 satisfies π/2<Θ<π , is
(a) (1, 2)
(b) (1, 2)
(c) (- 2, -1)
(d) (- 2, -1) < (1, 2)

Question 28. If the tangent at the point P on the circle x² + y² + 6x + 6y= 2 meets the straight line 5x – 2y + 6 = 0 at a point Q on the y-axis, then the length of PQ is
(a) 4
(b) 2√5
(c) 5
(d) 3√5Answer

C

Question 29. If the abscissae and ordinates of two points P and Q are roots of the equations x² + 2ax – b² = 0 and y² + 2py – q² = 0 respectively, then the equation of
the circle with PQ as diameter, is
(a) x² + y² + 2ax + 2py – b² – q² = 0
(b) x² + y² – 2ax – 2py + b² + q² = 0
(c) x² + y² – 2ax – 2py – b² – q² = 0
(d) x² + y² – 2ax + 2py + b² + q² = 0Answer

A

Question 30. The line 3x – 2y = kmeets the circle x² + y² = 4r² at only one point, if k² is
(a) 20 r²
(b) 52 r² 
(c) 52/9 r²
(d) 20/9 r²Answer

B

Question 31. A line through (0, 0) cuts the circle x² + y²– 2ax = 0 at A and B, then locus of the centre of the circle drawn AB as diameter is
(a) x² + y² – 2ay = 0
(b) x² + y² + ay = 0
(c) x² + y² + ax = 0
(d) x² + y² – ax = 0Answer

D

Question 32. Let PQand PS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point x on the circumference of the circle, then 2r equals
(a) √(PQ × RS)
(b) PQ + RS/2
(c) 2PQ . RS/PQ + RS
(d) (PQ² . RS² )/2Answer

A

Whoever needs to take the CBSE Class 11 Board Exam should look at this MCQ. To the Students who will show up in CBSE Class 11 Mathematics Board Exams, It is suggested to practice more and more questions. Aside from the sample paper you more likely had solved. These Conic Sections Class 11 MCQ are ready by the subject specialists themselves.

Question 33. If (a cos Θi , a sin Θi) , i = 1, 2, 3 represent the vertices of an equilateral triangle inscribed in a circle, then 
(a) cos Θ₁ cos Θ₂ cosΘ₃ = 0
(b) sec Θ₁ sec Θ₂ secΘ₃ = 0
(c) tan Θ₁ tan Θ₂ tanΘ₃ = 0
(d) cot Θ₁ cot Θ₂ cotΘ₃ = 0

Question 34. A straight line with slope 2 and y-intercept 5 touches the circle, x² + y² + 16x + 12 + c = 0 at a point Q. Then, the coordinates of Q are
(a) (-6, 11)
(b) (-9, -13)
(c) (-10, -15)
(d) (-6, -7)Answer

D

Question 35. The equation x² +  y² + 2gx + 2fy + c = 0 will represent a real circle, if
(a) g² + f² – c < 0
(b) g² + f² – c ≥ 0
(c) always
(d) None of theseAnswer

B

Question 36. The tangents to  x² +  y² = a² having inclinationsa andbintersect at P. If cot a + cot b = 0, then the locus of P is
(a) x + y = 0
(b) x – y = 0
(c) xy = 0
(d) None of theseAnswer

C

Question 37. The equation of a line inclined at an angle p/4 to the x-axis, such that the two circles x² + y² = 4, x² + y²– 10x – 14y + 65 = 0 intercept equal lengths on it, is
(a) 2x – 2y – 3 = 0
(b) 2x – 2y + 3 = 0
(c) x – y + 6 = 0
(d) x – y – 6 = 0

Question 38. Two points P and Qare taken on the line joining the points A(0 ,0) and B(3a, 0) such that AP = PQ = QB.
Circles are drawn on AP, PQand QB as diameters.
The locus of the points, the sum of the squares of the tangents from which to the three circles is equal to b2, is
(a) x² + y² – 3ax + 2a² – b² = 0
(b) 3x² + y² )- 9ax + 8a² – b² = 0
(c) x² + y² – 5ax + 6a² – b² = 0
(d) x² + y² – ax – b² = 0Answer

B

Question 39. Equation of chord of the circle x² + y² – 3x – 4y – 4 = 0 , which passes through the origin such that the origin divides it in the ratio 4 :1, is
(a) x = 0
(b) 24x + y = 0
(c) 7x + 24 y = 0
(d) 7x – 24 y = 0Answer

B

Question 40. In a ΔABC, right angled at A, on the leg AC as diameter, a semi-circle is described. If a chord joins A with the point of intersection D of the hypotenuse and the semi-circle, then the length of AC equal to
(a) AB x AD /√(AB² x AD²)
(b) AB x AD /AB + AD
(c) √(AB x AD)
(d) AB x AD /√(AB² – AD²)Answer

D

Question 41. Two perpendicular tangents to the circle x² + y² = a² meet at P. Then, the locus of P has the equation
(a) x² + y² = 2a²
(b) x² + y² = 3a²
(c) x² + y² = 4a²
(d) None of theseAnswer

A

Question 42. From a point on the circle x² + y² = a², two tangents are drawn to the circle x² + y² = a² sin2α.The angle between them is
(a) α
(b) α/2
(c) 2α
(d) None of these

Question 43. If a > 2 b > 0, then the positive value of m for which y = mx – b√(1 + m²) is a common tangent to x² + y² = b² and (x – a)² + y² = b², is

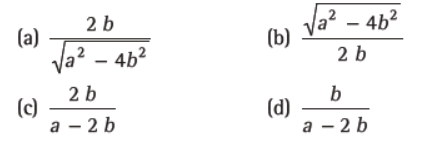
Answer

A

Question 45. The length of the diameter of the circle which touches the x-axis at the point (1, 0) and passes through the point (2, 3) is 
(a) 10/3
(b) 3/5
(c) 6/5
(d) 5/3Answer

A

Question 46. The two circles x y ax 2 + 2 = and x y c 2 + 2 = 2, (c > 0) touch each other if 
(a) |a |= c
(b) a = 2c
(c) |a |= 2c
(d) 2|a |= cAnswer

A

Question 47. The equation of the circle passing through the points (1,0) and (0, 1) and having the smallest radius is
(a) x² + y² +x + y – 2 = 0
(b) x² + y² -2x – 2y + 1 = 0
(c) x² + y² -x – y = 0
(d) x² + y² +2x + 2y + 7 = 0

Question 48. The equation of a circleC₁ is x² + y² = 4.The locus of the intersection of orthogonal tangents to the circle is the curve C₂ and the locus of the intersection of perpendicular tangents to the curve C₂ is the curve C₃. Then,
(a) C₃ is a circle  
(b) the area enclosed by the curve C₃ is 8p
(c) C₂ and C₃ are circles with the same centre
(d) None of the aboveAnswer

(a,c)

Question 49. The equation of the tangents drawn from the origin to the circle x² + y² – 2rx – 2hy + h² = 0, are
(a) x = 0
(b) y = 0    
(c) (h² – r² )x – 2rhy = 0
(d) (h² – r² )x + 2rhy = 0Answer

(a,c)

Question 50. If P = (2, 3), then the centre of circumcircle of ΔQRS is
(a) (2/13 .7/26) 
(b) (2/13 .3/26) 
(c) (3/13 .9/26) 
(d) (3/13 .2/13) Answer

C

Question 51. The circle passing through (1, -2) and touching the axis to x at (3, 0) also passes through the point
(a) (-5,2)
(b) (2, -5)
(c) (5, – 2)
(d) (-2,5)

Question 52. If the lines 3x – 4 y – 7 = 0 and 2x – 3 y – 5 = 0 are two diameters of a circle of area 49p sq units, the equation of the circle is 
(a) x² + y² =2x – 2y – 62 = 0
(b) x² + y² =2x + 2y – 62 = 0
(c) x² + y² =2x + 2y – 47 = 0
(d)x² + y² =2x – 2y – 47 = 0Answer

C

Question 53. If the pair of lines ax² + 2(a+b)xy + by2 = 0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector, then 
(a) 3a² + 2ab + 3b² = 0
(b) 3a² + 10ab + 3b² = 0
(c) 3a₂ – 2ab + 3b² = 0
(d) 3a² – 10ab + 3b² = 0Answer

A

Question 54. A circle touches the x-axis and also touches the circle with centre at (0, 3) and radius 2. The locus of the centre of the circle is 
(a) a parabola
(b) a hyperbola
(c) a circle
(d) an ellipseAnswer

A

Question 55. The intercept on the line y = x by the circle x² + y² – 2x = 0 is AB. Equation of the circle on ABas a diameter is 
(a) x² + y² – x – y = 0
(b) x² + y² – x + y = 0
(c) x² + y² + x + y = 0
(d) x² + y² + x – y = 0Answer

A

Question 56. How many common tangents can be drawn to the following circles x² + y² = 6 and x² + y² + 6x + 2y + 1 = 0 ? 
(a) 4
(b) 3
(c) 2
(d) 1

Question 57. The circle x² + y² – 10x – 14 y + 24 = 0 cuts an intercepts on y-axis of length
(a) 5
(b) 10
(c) 1
(d) None of theseAnswer

B

Question 58. If the line 3x – 4 y – k = 0, (k > 0) touches the circle x² + y² – 4x + 10y + 5 = 0= 0 at (a, b) , then k + a + b is equal to
(a) 20
(b) 22
(c) -30
(d) -28Answer

A

Question 59. A variable circle passes through the fixed point A( p, q) and touches x-axis. The locus of the other end of the diameter through A is 
(a) (x – p)² = 4qy 
(b) (x – q)² = 4py 
(c) ( y – p)² = 4qx 
(d) ( y – q)² = pxAnswer

A

Question 60. The point diameterically opposite to the point P(1, 0) on the circle x² + y² +2x + 2y – 3 = 0 is
(a) (3, 4)
(b) (3, – 4)
(c) (- 3, 4)
(d) (- 3, – 4)Answer

D

Question 61. Consider a family of circles which are passing through the point (- 1, 1) and are tangent to x-axis. If (h, k) is the centre of circle, then 
(a) k ≥ 1/2
(b) – 1/2 ≤ k ≤ 1/2
(c) k ≤ 1/2
(d) 0 < k < 1/2Answer

A

Question 62. Any chord of the circle x² + y² = 25 subtends a right angle at the centre. Then, the locus of the centroid of the triangle made by the chord and a moving point P on the circle is
(a) parabola
(b) circle
(c) rectangular hyperbola
(d) ellipseAnswer

B

Question 63. LetC be the circle with centre (0, 0) and radius 3. The equation of the locus of the mid-points of the chords of the circleC that subtend an angle 2p/3 at its centre is
(a) x² + y² =27/4
(b) x² + y² =9/4
(c) x² + y² =3/2
(d)  x² + y² =1

You can easily get good marks If you study with the help of Class 11 Conic Sections MCQ. We trust that information provided is useful for you. NCERT MCQ Questions for Class 11 Conic Sections PDF Free Download would without a doubt create positive results. 

We hope the information shared above in regards to MCQ on Conic Sections Class 11 with Answers has been helpful to you. If you have any questions regarding CBSE Class 11 Mathematics Solutions MCQs Pdf, write a comment below and we will get back to you as soon as possible.