Polynomials Class 9 MCQ is one of the best strategies to prepare for the CBSE Class 9 Board exam. If you want to complete a grasp concept or work on one’s score, there is no method except constant practice. Students can improve their speed and accuracy by doing more Polynomials class 9 MCQ which will help them all through their board test.
Polynomials Class 9 MCQ Questions with Answer
Class 9 Math MCQ with answers are given here to Chapter 2 Polynomials. These MCQs are based on the latest CBSE board syllabus and relate to the latest Class 9 Math syllabus. By Solving these Class 9 MCQs, you will be able to analyze all of the concepts quickly in the Chapter and get ready for the Class 9 Annual exam.
Learn Polynomials Class 9 MCQ with answers pdf free download according to the latest CBSE and NCERT syllabus. Students should prepare for the examination by solving CBSE Class 9 Polynomials MCQ with answers given below.
Question 1. If the sum of the product of the zeroes taken two at a time of the polynomial f(x) = 2x3 – 3x2 + 4tx – 5 is –8, then the value of t is _______.
(A) 2
(B) 4
(C) –2
(D) – 4
Answer
D
Question 2. If a and b are the roots of the quadratic equation x2 + px + 12 = 0 with the condition a – b = 1, then the value of ‘p’ is _______.
(A) 1
(B) 7
(C) –7
(D) 7 or –7
Answer
D
Question 3. What will be the value of p(3), if 3 is one of zeroes of polynomial p(x) = x3 + bx + D?
(A) 3
(B) D
(C) 27
(D) 0
Answer
D
Question 4. px3 + qx2 + rx + s = 0 is said to be cubic polynomial, if _______.
(A) s ≠ 0
(B) r ≠ 0
(C) q ≠ 0
(D) p ≠ 0
Answer
D
Question 5. If sum of all zeros of the polynomial 5x2 – (3 + k)x + 7 is zero, then zeroes of the polynomial 2x2 – 2(k + 11)x + 30 are
(A) 3, 5
(B) 7, 9
(C) 3, 6
(D) 2, 5
Answer
A
Question 6. When x3 – 3x2 + 3x + 5 is divided by x2 – x + 1, the quotient and remainder are _______.
(A) x + 2, 7
(B) x – 2, –7
(C) x – 2, 7
(D) x + 2, –7
Answer
C
Question 7. A cubic polynomial with sum of its zeroes, sum of the product of its zeroes taken two at a time and the product of its zeroes as –3, 8, 4 respectively, is _______.
(A) x3 – 3x2 – 8x – 4
(B) x3 + 3x2 – 8x – 4
(C) x3 + 3x2 + 8x – 4
(D) x3 – 3x2 – 8x + 4
Answer
C
Question 8. If p, q are the zeroes of the polynomial f(x) = x2 + k(x – 1) – c, then (p – 1)(q – 1) is equal to _______.
(A) c –1
(B) 1 – c
(C) c
(D) 1 + c
Answer
B
Question 9. The factorisation of (2a – b)3 + (b – 2c)3 + 8(c – a)3 is :
(A) (2a – b)(b – 2c)(c – a)
(B) 3(2a – b)(b – 2c)(c – a)
(C) 6(2a – b)(b – 2c)(c – a)
(D) 2a × b × 2c
Answer
C
Question 10. If x1/3+y1/3+z1/3 = 0 then which one of the following expression is correct :
(A) x3 + y3+ z3 = 0
(B) x + y + z = 3x1/3+y1/3+z1/3
(C) x + y + z = 3xyz
(D) x3 + y3+ z3 = 3xyz
Answer
B
Question 11. The volume of a cube is given by the expression 27x3 + 8y3 + 54x2y + 36xy2. What is the expression for the side length of the cube?
(A) 3x + 2y
(B) 3x – 2y
(C) 9x – 8y
(D) 9x + 8y
Answer
A
Question 12. In which of the following, (x + 2) is a factor ?
(A) 4x3 – 13x + 6
(B) x3+ x2 + x + 4
(C) 4x3 + 13x – 25
(D) – 2x3 + x2 – x – 19
Answer
A
Question 13. Degree of the polynomial (x3 – 2) (x2 + 11) is :
(A) 6
(B) 5
(C) 3
(D) 2
Answer
B
Question 14. Which of the following is a binomial in y ?
(A) y2 + √2
(B) y + 1/y +2
(C) √y + √2y
(D) y√y + 1
Answer
A
Question 15. Which of these is obtained by factorizing the polynomial 10x2 – 9x + 2 ?
(A) (2x – 1)(5x – 2)
(B) (2x – 1)(5x + 2)
(C) (2x + 1)(5x + 2)
(D) (2x + 1)(5x – 2)
Answer
A
Question 16. The zeroes of the polynomial p(x) = x2 – (2k + 1)x + 16 are positive integers. Given that k is an integer, which of these is equivalent to the polynomial?
(A) (x – 1)(x + 16)
(B) (x – 1)(x – 16)
(C) (x – 2)(x – 8)
(D) (x – 4)(x – 4)
Answer
B
Question 17. If x2 + kx + 6 + (x + 2)(x + 3) for all x, the value of k is :
(A) 1
(B) – 1
(C) 5
(D) 3
Answer
C
Question 18. 8 is a polynomial of degree :
(A) 1
(B) 1/2
(C) 8
(D) 0
Answer
D
Question 19. If one zero of the polynomial f(x) = (k2 + 4) x2 + 13x + 4k is reciprocal of the other, then k is equal to _______.
(A) 2
(B) –2
(C) 1
(D) –1
Answer
A
Question 20. A polynomial of the form ax5 + bx3 + cx2 + dx + e has at most _______ zeroes.
(A) 3
(B) 5
(C) 7
(D) 11
Answer
B
Question 21. What should be subtracted from f(x) = 6x3 + 11x2 – 39x – 65 so that f(x) is exactly divisible by x2 + x – 1?
(A) 38x + 60
(B) –38x – 60
(C) –19x – 30
(D) 9x + 10
Answer
B
Question 22. Which of the following graph has more than three distinct real roots?

Answer
C
Whoever needs to take the CBSE Class 9 Board Exam should look at this MCQ. To the Students who will show up in CBSE Class 9 Math Board Exams, It is suggested to practice more and more questions. Aside from the sample paper you more likely had solved. These Polynomials Class 9 MCQ are ready by the subject specialists themselves.
Question 23. If α, β be two zeroes of the quadratic polynomial ax2 + bx – c = 0, then find the value of
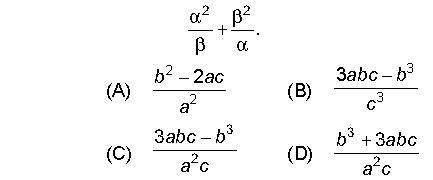
Answer
D
Question 24. If α and β are the roots of the equation 2x2 – 7x + 8β = 0, then the equation whose roots are(3α – 4β) and (3β – 4α) is _______.
(A) 2x2 + 7x + 98 = 0
(B) x2 + 7x + 98 = 0
(C) 2x2 – 7x – 98 = 0
(D) 2x2 – 7x + 98 = 0
Answer
A
Question 25. For x2 + 2x + 5 to be a factor of x4 + αx2 + β, the values of a and b should respectively be _______.
(A) 2, 5
(B) 5, 25
(C) 6, 25
(D) 5, 2
Answer
C
Question 26. Raghav had `(6x3 + 2x2 + 3x) and he bought (4x2 + 3) shirts. The price of each shirt is `(x + 5). How much money is left with Raghav?
(A) `(2x3 – 18x2 – 15)
(B) `(4x2 + 2x + 3)
(C) `(x3 – 3x)
(D) `(2x3 + 2x2 – 15)
Answer
A
Question 27. Two different container contains (2x3 + 2x2 + 3x + 3) L and (4x3 – 2x2 + 6x – 3)L water. What is biggest measure that can measure both quantities exactly?
(A) (x2 + 2x) L
(B) (2x2 + 3) L
(C) (2x – 1) L
(D) (x + 1) L
Answer
B
Question 28. Area of a triangular field is (x4 – 6x3 – 26x2 + 138x – 35) m2 and base of the triangular field is (x2 – 4x + 1) m. Find the height of the triangular field.
(A) 2(x2 – 2x – 35) m
(B) 1/2 (x2 − 2x − 35) m
(C) 2(3x2 – x – 4) m
(D) 1/2(3x2 − x − 4) m
Answer
A
Question 29. A r e c t angular garden o f length (2x3 + 5x2 – 7) m has the perimeter (4x3 – 2x2 + 4) m. Find the breadth of the garden.
(A) (6x2 – 9) m
(B) (–6x2 + 9) m
(C) (2x3 – 7x2 + 11) m
(D) (6x3 + 7x2 + 9) m
Answer
B
Question 30. Which of the following options hold? Statement – I : If p(x) and g(x) are two polynomials with g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that p(x) = g(x) × q(x) + r(x), where degree of r(x) is greater than degree of g(x).
Statement – II : When 4x5 + 3x3 + 2x2 + 8 is divided by 4x2 + 2x + 1, then degree of remainder is 1.
(A) Both Statement – I and Statement – II are true.
(B) Statement – I is true but Statement – II is false.
(C) Statement – I is false but Statement – II is true.
(D) Both Statement – I and Statement – II are false
Answer
C
Question 31. Obtain all the zeroes of the polynomial f(x) = 3x4 + 6x3 – 2x2 – 10x – 5, if two of its zeros are √5/3 and− √5/3
(A) 1, –1
(B) 1, 1
(C) –1, –1
(D) 1, 0
Answer
C
Question 32. Length and breadth of a rectangular park are (3x2 + 2x) m and (2x3 – 3) m respectively. Find the area of the park, when x = 3.
(A) 1924 m2
(B) 1492 m2
(C) 1881 m2
(D) 1683 m2
Answer
D
Question 33. Find the roots of ax2 + bx + 6, if the polynomial x4 + x3 + 8x2 + ax + b is exactly divisible by x2 + 1.
(A) –1, 3
(B) 2, 5
(C) –1, –6
(D) –3, 2
Answer
C
Question 34. If 1 and –1 are zeroes of polynomial Lx4 + Mx3 + Nx2 + Rx + P, then Find :
(i) L + N + P
(ii) M + R
(iii) M3 + R3
(i) (ii) (iii)
(A) 1 1 –1
(B) 0 –1 0
(C) 0 0 0
(D) –1 1 1
Answer
C
Question 35. The degree of a non-zero constant polynomial is :
(A) 1
(B) –1
(C) 0
(D) –2
Answer
C
Question 36. Match the following.
Column – I Column – II
(P) If one of the zero of the polynomial (i) 1
f(x) = (k2 + 4)x2 + 13x + 4
is reciprocal of the other, then k is equal to
(Q) Sum of the zeroes of the polynomial (ii) 0
is 3, then k is equal to f(x) = 2x3 + kx2 + 4x + 5
(R) If the polynomial f(x) = ax3 + bx – c (iii) –6
is exactly divisible by g(x) = x2 + bx + c,
then ab is equal to
(A) (P) → (iii); (Q) → (i); (R) → (ii)
(B) (P) → (ii); (Q) → (iii); (R) → (i)
(C) (P) → (i); (Q) → (iii); (R) → (ii)
(D) (P) → (ii); (Q) → (i); (R) → (iii)
Answer
B
Case based MCQs
Read the following passage and answer the questions.
Three friends A, B and C of locality decided to start a business with a capital represented by a polynomial x3 + kx2 – x + 5, which is the product of their shares, such that shares of A, B and C are in decreasing order.
Question 37. If share of A in the capital polynomial is (x + 1), then value of k is
(A) 1
(B) –1
(C) 5
(D) –5
Answer
D
Question 38. If x = 20, then total capital (in ) is
(A) 10025
(B) 10005
(C) 9995
(D) 9985
Answer
D
Question 39. Share of B in the capital is
(A) (x + 1)
(B) (x – 1)
(C) (x – 2)
(D) (x – 5)
Answer
B
Question 40. The polynomial is a
(A) constant polynomial
(B) linear polynomial
(C) quadratic polynomial
(D) cubic polynomial
Answer
D
Question 41. Share of C in the capital is
(A) (x – 1)
(B) (x – 3)
(C) (x – 5)
(D) (x + 5)
Answer
C
Read the following passage and answer the questions.
Some of the students of class IX contributed some money to help in the education of needy students. Their total contribution is in the form of a polynomial x12 – y12, which is the product of the contributions of all the students. These contributions are in the form of irreducible factors of the total contribution.
Question 42. Number of students, who contributed the money, is
(A) 3
(B) 4
(C) 5
(D) 6
Answer
D
Question 43. Factorisation of x12 – y12 is
(A) (x – y) (x + y) (x2 + y2 + xy) (x4 + y4 – x2y2)
(B) (x – y) (x2 + y2 – xy) (x4 + y4 – x2y2)
(C) (x + y) (x – y) (x2+ y2) (x2 + y2– xy) (x2 + y2 + xy) (x4 + y4 – x2y2)
(D) (x + y) (x – y) (x2 + y2) (x2 + y2– xy) (x4 + y4 + x2y2)
Answer
C
Question 44. If x = 2 and y = 1, then the total contribution (in ) is
(A) 4195
(B) 4095
(C) 4083
(D) 3993
Answer
B
You can easily get good marks If you study with the help of Class 9 Polynomials MCQ. We trust that information provided is useful for you. NCERT MCQ Questions for Class 9 Polynomials PDF Free Download would without a doubt create positive results.
We hope the information shared above in regards to MCQ on Polynomials Class 9 with Answers has been helpful to you. If you have any questions regarding CBSE Class 9 Math Solutions MCQs Pdf, write a comment below and we will get back to you as soon as possible.
Frequently Asked Question (FAQs)
How many MCQ questions are there in Class 9 Chapter 2 Math?
In Class 9 Chapter 2 Math, we have provided 44 Important MCQ Questions, But in the future, we will add more MCQs so that you can get good marks in the Class 9 exam.
Can we score good marks in Class 9 Math with the help of Polynomials MCQ Questions?
Yes, MCQ Question is one of the best strategies to make your preparation better for the CBSE Board Exam. It also helps to know the student’s basic understanding of each Chapter. So, You can score good marks in the Class 9 Math exam.