Class 12 Mathematics Chapter 12 Linear Programming MCQ Questions with Answer

Class 12 Linear Programming MCQ is one of the best strategies to prepare for the CBSE Class 12 Board exam. If you want to complete a grasp concept or work on one’s score, there is no method except constant practice. Students can improve their speed and accuracy by doing more MCQ on Linear Programming Class 12, which will help them all through their board test.

Class 12 Linear Programming MCQ Questions with Answer

Class 12 Maths MCQ with answers are given here to Chapter 12 Linear Programming . These MCQs are based on the latest CBSE board syllabus and relate to the latest Class 12 Mathematics syllabus. By Solving these Class 12 MCQs, you will be able to analyze all of the concepts quickly in the chapter and get ready for the Class 12 Annual exam.

Learn Linear Programming Class 12 MCQ with answers pdf free download according to the latest CBSE and NCERT syllabus. Students should prepare for the examination by solving CBSE Class 12 Mathematics Linear Programming MCQ with answers given below.

Question 1. The solution set of the inequation 3x + 2y > 3 is
(a) half plane not containing the origin
(b) half plane containing the origin
(c) the point being on the line 3x + 2y = 3
(d) None of these

Question 2. In an LPP, if the objective function Z = ax + by has the same maximum value on two corner points of the feasible region, then the number of points of which Zmax occurs is
(a) 0
(b) 2
(c) finite
(d) infinite

Question 3. The feasible region for an LPP is shown below:

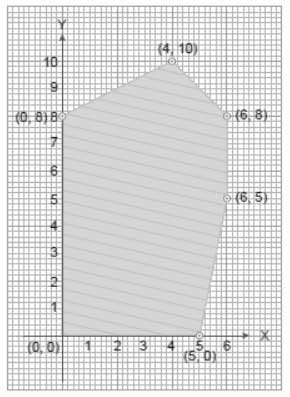
Let Z = 3x – 4y be the objective function. Minimum of Z occurs at
(a) (0, 0)
(b) (0, 8)
(c) (5, 0)
(d) (4, 10)

Question 4. Which of the following statement is correct?
(a) Every LPP admits an optimal solution.
(b) Every LPP admits unique optimal solution.
(c) If a LPP gives two optimal solutions it has infinite number of solutions.
(d) None of these

Question 5. If the constraints in a linear programming problem are changed
(a) solution is not defined
(b) the objective function has to be modified
(c) the problems is to be re-evaluated
(d) none of these

Question 6. The maximum value of Z = 4x + 3y subjected to the constraints 2x + 3y ≤ 18, x + y ≥ 10; x, y ≥ 0 is
(a) 36
(b) 40
(c) 20
(d) none of these

Question 7. Corner points of the feasible region determined by the system of linear constraints are (0, 3),
(1, 1) and (3, 0). Let Z = px + qy, where p, q > 0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is
(a) p = 2q
(b) p = q/2
(c) p = 3q
(d) p = q

Question 8. The optimal value of the objective function is attained at the points
(a) given by intersection of inequation with y-axis only.
(b) given by intersection of inequation with x-axis only.
(c) given by corner points of the feasible region.
(d) none of these

Question 9. The objective function Z = 4x + 3y can be maximised subjected to the constraints 3x + 4y ≤ 24,8x + 6y ≤ 48, x ≤ 5, y ≤ 6; x, y ≥ 0
(a) at only one point
(b) at two points only
(c) at an infinite number of points
(d) none of these

Question 10. Feasible region (shaded) for a LPP is shown in the given figure. Minimum of z = 4x + 3y occurs at the point

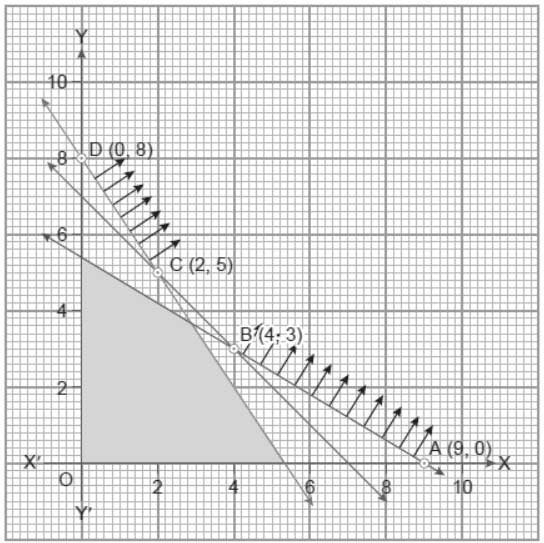
(a) (0, 8)
(b) (2, 5)
(c) (4, 3)
(d) (9, 0)

Whoever needs to take the CBSE Class 12 Board Exam should look at this MCQ. To the Students who will show up in CBSE Class 12 Mathematics Board Exams, It is suggested to practice more and more questions. Aside from the sample paper you more likely had solved. These Linear Programming Class 12 MCQ are ready by the subject specialists themselves.

Fill in the blanks

Question 1. In a LPP, the objective function is always ____________.     

Question 2. The corner points of the feasible region of an LPP are (0, 0), (0, 8), (2, 7), (5, 4) and (6, 0). The maximum profit P = 3x + 2y occurs at the point ____________. 

Question 3. In a LPP, the linear function which has to be maximised or minimised is called a linear ____________ function. 

Question 4. If the feasible region for a LPP is ____________, then the optimal value of the objective function Z = ax + by may or may not exist.   

Question 5. The common region determined by all the linear constraints of a LPP is called the ____________ region.    

Question 6. In a LPP, the inequalities or restrictions on the variables are called ____________.   

Question 7. A corner point of a feasible region is a point in the region which is the ____________ of two boundary lines. 

Question 8. The feasible region for an LPP is always a ____________ polygon.     

Question 9. The maximum value of Z = 6x + 16y satisfying the conditions x + y $ 2 , x $ 0, y $ 0 is ____________.     

You can easily get good marks If you study with the help of Class 12 Linear Programming MCQ. We trust that information provided is useful for you. NCERT MCQ Questions for Class 12 Linear Programming PDF Free Download would without a doubt create positive results.

We hope the information shared above in regards to MCQ on Linear Programming Class 12 with Answers has been helpful to you. if you have any questions regarding CBSE Class 12 Linear Programming MCQ Pdf, write a comment below and we will get back to you as soon as possible.